Composeを使ったコーディング - most adequate guide Chapter 5のテキトーな訳
このページの趣旨
下記ページの、かなり「大雑把」に、「私が興味を持ったところだけ」を「雰囲気」で翻訳したものです。
mostly-adequate.gitbooks.io Chapter 05: Coding by Composing
原文をかなり崩して書いている(原文にない単語、文章を追加したりしている箇所もある)ので、翻訳とすら、呼べないものかもしれません。
違和感を感じたら、原文を参照することをおすすめします。
Chapter5: Composeを使ったコーディング
関数を組み合わせて使いやすい関数を作ろう
下記がcomposeの汎用的な定義です。
const compose = (...fns) => (...args) =>
fns.reduceRight((res, fn) => [fn.call(null, ...res)], args)[0];ただ、現時点で、これがわからなくても大丈夫です。この表記方法は、ものすごく難解な表記方法なので、理解できなくても当たり前です。
そこで、composeがどういうものか理解するために、いったん汎用的な表現から離れます。まずは、2つの関数を結合(compose)する単純な例を見てみましょう。
いったん、具体的な例でcomposeを理解した後に、それを抽象化して考えてみてください。そうすれば、関数がいくつあってもcomposeが動くことが理解できると思います(それを証明することもできます)。
まずは、composeを理解しやすい形で書いてみましょう。
const compose2 = (f, g) => x => f(g(x));fとgはfunctionで、xは値です。xは、それらのfunctionに(次々と)渡されていく値です。
結合(composition)という演算は、functionを飼育するイメージにも感じられます。たとえば、あなたは、functionのブリーダーです。組み合わせたい2つの関数を選び・混ぜ合わせて、新しいfunctionを作り出すのです。
それでは、話を元に戻しましょう。composeは次のように使います。
const toUpperCase = x => x.toUpperCase();
const exclaim = x => `${x}!`;
const shout = compose(exclaim, toUpperCase);
shout('send in the clowns'); // "SEND IN THE CLOWNS!"2つのfunctionを結合すると、1つの新しいfunctionが得られます。これは、次のように理解することができます。
2つの同じ型(今回の例ではfunction)の「もの」を結合すると、それとまったく同じ型の新しい「もの」ができあがる
2つのレゴブロックを組み合わせても、リンカーンログ(丸太を組み合わせてログハウスを作るおもちゃ)にはならないということです。今回の「結合演算」の根底には、ある「基本的な法則」が潜んでいます。それについては、後で考えていきましょう。
さて、先ほどのcomposeの定義を見ると、gが先に実行され、fが後に実行されることがわかります。要は、データxは、右から左に流れていくことになります。
さて、このcomposeを使った書き方は、関数呼び出しをネストさせるよりも、はるかに読みやすいものになります。実際、composeを使わない場合、先ほどの式は次のように書くことになります。
const shout = x => exclaim(toUpperCase(x));この書き方だと、内側から外側の順に関数が実行されていきます。一方で、composeを使えば、右から左に関数が実行されます。
次に、シーケンス(配列など)に対する処理を見ていきましょう。
const head = x => x[0];
const reverse = reduce((acc, x) => [x].concat(acc), []);
const last = compose(head, reverse);
last(['jumpkick', 'roundhouse', 'uppercut']); // 'uppercut'reverseはリストを逆順に並べ替え、headは、最初の要素を取得します。この2つを組み合わせた結果、(効率的ではありませんが)正しく計算できるlast関数を作ることができました。なお、composeの中の関数の並び順は重要です。並び順が変わると結果が変わる場合があることに注意してください。
また、関数を左から右に適用していくようなcomposeに似た関数を定義することもできます。現状の定義のほうが、数学でいう結合の概念に違いものになります。実は結合(compose)という概念は、数学から来ているのです。
さて、composeは次のような性質を持っています。
// 結合法則を満たす
compose(f, compose(g, h)) === compose(compose(f, g), h);composeが結合法則を満たすということは、3つの関数を結合するときに、最初に、どの2つの関数を結合しても構わないということです。
たとえば、先ほどの例で、さらに最後に、抽出した文字列を大文字に変換することを考えてみましょう。このとき、次のどちらで書いてもかまいません。
compose(toUpperCase, compose(head, reverse));
// または
compose(compose(toUpperCase, head), reverse);どのようにcomposeをするくくりを変えても、計算結果は変わりません。
ですから、次のように関数を可変個指定するようなcomposeを書くこともできます。
// 今まで、2つの関数だけを結合してきました。
// でもcomposeは結合法則を満たすので、
// composeの引数に関数を何個書いても構いません(計算結果は変わりません)。
// どれを最初に結合するかは、composeの実装で自由に決められます。
const arg = ['jumpkick', 'roundhouse', 'uppercut'];
const lastUpper = compose(toUpperCase, head, reverse);
const loudLastUpper = compose(exclaim, toUpperCase, head, reverse);
lastUpper(arg); // 'UPPERCUT'
loudLastUpper(arg); // 'UPPERCUT!'結合法則が成り立っているので、このように、(右から左に適用する関数をカンマで区切って指定するという)柔軟な表記をすることができます。
もちろん、(どれを最初に結合しても)常に同じ計算結果が得られるので安心して使うことができます。
なお、少し複雑な可変個引数についての定義はこの本のサポートライブラリに含まれています。これは、lodash、underscoreやramdaなどに含まれている通常の定義と同じです。
さて、結合法則を満たすことによるメリットの1つに「複数の関数をcomposeしたもの」を、composeの引数として指定することができる、ということが挙げられます。
この性質を使って、先ほどの例をリファクタリングしてみましょう。
const loudLastUpper = compose(exclaim, toUpperCase, head, reverse);
// -- または --------
const last = compose(head, reverse);
const loudLastUpper = compose(exclaim, toUpperCase, last);
// -- または --------
const last = compose(head, reverse);
const angry = compose(exclaim, toUpperCase);
const loudLastUpper = compose(angry, last);
// 他にも様々な書き方がありますどの方法を選ぶべきかについては、正解・不正解はありません。好きな方法で、レゴブロックを組み立てるように、関数を組み立ててください。
通常は、last、angryなど、再利用できるような単位で、関数をまとめていくといいでしょう。
もし、FowlerのRefactoringという本を読んだことがあるのであれば、この操作は、関数の抽出と同じものだと感じられるかもしれません。もっとも、今回の方法であれば「オブジェクトの状態をまったく意識しないで済む」という点は、違っていますが。
Pointfree styleによるプログラミング
Pointfree styleとは、データそのものについての記述をしないプログラミング手法のことを言います。これは、関数を定義するときに、関数が操作するデータについての記述をしない、ということでもあります。
関数を第一級オブジェクトとして扱うこと、カリー化、結合、これらをうまく組み合わせることで、この手法ができあがっています。
// pointfreeではありません。なぜならデータを表す「word」という変数が出てきているからです
const snakeCase = word => word.toLowerCase().replace(/\s+/ig, '_');
// pointfree
const snakeCase = compose(replace(/\s+/ig, '_'), toLowerCase);replaceに対して、どのように部分適用をしているでしょうか?replaceは3つの引数を取る関数で、そのうち2つの引数をあらかじめ部分適用して、composeに入れる段階では、残りの1つの引数だけを受け取ればいい状態になっています。そして、composeには「1つの引数をとる関数」を指定して、それらの関数に対してデータを次々と流していっているのです。
このように、カリー化を使って関数を準備することで、データを受け取り、処理をして、次の関数に渡すしています。
また、別の注目点として、pointfree版では、関数について記述をするときに「データについての記述」をしていません。一方で、pointfreeでないほうは、最初にwordというデータを使うための記述が必要になります。
ヒント:
replace、toLowerCaseを、Pointfreeな書き方で定義したものがAppendix C - Pointfree Utilitiesの中に入っています。ぜひ、見てみてください。
それでは、別の例も見てみましょう。
// pointfreeではありません。なぜならデータを表す「name」という変数が出てきているからです
const initials = name => name.split(' ').map(compose(toUpperCase, head)).join('. ');
// pointfree
// 注:今回は、Chapter9で出てくる'join'の代わりに、appendixに出てくる'intercalate'を使っています。
const initials = compose(intercalate('. '), map(compose(toUpperCase, head)), split(' '));
initials('hunter stockton thompson'); // 'H. S. T'pointfree styleのコードでは、今回も「データの名前」は不要なので取り除いています。その結果、簡潔で汎用的な書き方になっています。
pointfree styleは、関数型によるコーディングをするときに、入力から出力にうまく変換できる、小さい関数があるかどうかを判定する、ちょうどいい指標となります。たとえば、pointfree styleでは、whileループを作ることはできません。
ただし、pointfree styleを使うのは、諸刃の剣でもあり、ときどき意図が掴みにくくなるときもあります。ですから、すべての関数型によるコーディングを、pointfree styleにより行う必要はありません。
pointfree styleを使えるときは使えばいいですし、使えないときには通常の関数を使いましょう。
デバッグ
ここで、composeを使う場合に、よくある間違いのパターンを紹介します。
それは、mapのような2つの引数を取る関数を、1つ目の引数に部分適用をしない状態でcomposeをしてしまう、というものです。
// NG:angryの引数に「配列」を渡し、mapの1つ目の引数に「よくわからない何か」を渡して部分適用しています
const latin = compose(map, angry, reverse);
latin(['frog', 'eyes']); // error
// OK:それぞれのfunctionは、1つの引数を受け取る関数になっています
const latin = compose(map(angry), reverse);
latin(['frog', 'eyes']); // ['EYES!', 'FROG!'])次の例で、実際にデバッグをしてみましょう。
もし、composeが、うまくいかなくなった場合には、(非純粋関数ですが)ログ出力をする関数を定義・使用して、何が起きているのか見てみましょう。
const dasherize = compose(
intercalate('-'),
toLowerCase,
split(' '),
replace(/\s{2,}/ig, ' '),
);
dasherize('The world is a vampire');
// TypeError: s.toLowerCase is not a function何か誤りがあるようなので、trace関数を定義して使ってみます。
const trace = curry((tag, x) => { console.log(tag, x); return x;});
const dasherize = compose(
intercalate('-'),
toLowerCase,
trace('after split'), split(' '),
replace(/\s{2,}/ig, ' '),
);
dasherize('The world is a vampire');
// after split [ 'The', 'world', 'is', 'a', 'vampire' ] // TypeError: s.toLowerCase is not a function配列の各要素に対してtoLowerCaseで処理をしたいのですから、mapをする必要があることがわかります。
const dasherize = compose(
intercalate('-'),
map(toLowerCase), split(' '),
replace(/\s{2,}/ig, ' '),
);
dasherize('The world is a vampire'); // 'the-world-is-a-vampire'このように、trace関数を使うことで、デバッグ用に、ある時点でのデータの内容を見ることができます。ちなみに、HaskellやPureScriptにも、開発を楽にするために、同じような関数があります。
さて、Composition(結合)は、プログラムを作るためのツールになります。また、(運がいいことに)強力な理論により、うまくいくことが裏付けられています。
それでは、この理論を見ていきましょう。
圏論
圏論は、数学の中で抽象的な分野の一つで、集合論、型理論、群論、論理学などの様々な分野の構造を統一的に扱うものです。
圏論では、主に、対象、射、変換を扱います。これらは、プログラミングに非常に近く、概念を対応付けることができます。次の表では、それぞれの分野で扱われる概念で、同じ概念であるものをまとめています。
| 型理論 | 論理学 | 集合論 | homotopy |
|---|---|---|---|
| 命題 | 集合 | space | |
| 証明 | 要素 | point | |
| 命題 | 集合族 | fibration | |
| 条件付き証明 | family of elements | section | |
| disjoint union | coproduct | ||
| set of pairs | product space | ||
| set of functions | function space | ||
| disjoint sum | total space | ||
| product | space of sections | ||
| (等号) | path space |
決して、あなたを怖がらせようとして書いたわけではありません。また、これらの概念すべてに慣れてほしい、と思っているわけでもありません。
伝えたいことは、様々な分野で概念が重複しているということです。そして、これを見れば、圏論が、様々な分野の概念を統一しようとしている理由がわかるのではないかと思います。
圏とは何か?
圏論では、圏と呼ばれるものがあります。圏は、次のようなもの(の集まり)として定義されます。
- 対象(の集まり)
- 射(の集まり)
- 射は合成できること
- 射の中に恒等射と呼ばれる射があること
圏論は、抽象的なので、様々なものにあてはめることができます。ただ、今回は、プログラミングに関連する概念である「型」と「関数」にあてはめてみましょう。
対象(の集まり)
「対象」は「データ型」に対応します。たとえば、String、Boolean、Number、Objectなどといったものです。
よく、データ型のことを、取り得る値の集合、とみなして考えることもあります。たとえば、Booleanを[true, false]という値の集合として見たり、Numberを、すべての取り得る数値の集合として見ることができます。
型を集合として扱うと、集合論の知識を使って考えることができるようになるので、有用です。
射(の集まり)
「射」は、普通の「純粋関数」に対応します。
射は合成できること
すでにわかっているかもしれませんが、「射の合成」は、さきほど導入したcomposeに対応します。先ほど書いたとおり、composeは、結合法則を満たします。
これは偶然ではありません。圏論の「射の合成」にあてはまるのであれば、この性質を必ず持っている必要があるのです。
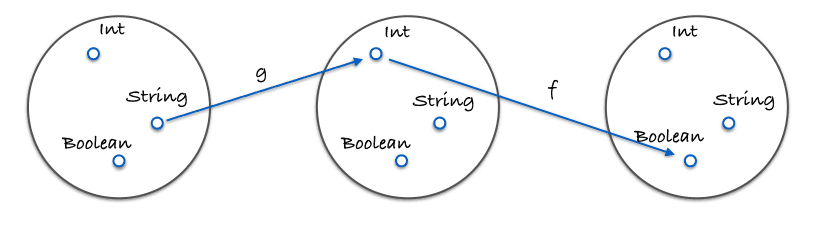
次の図は、結合のイメージを表しています。
具体的なコード例は、次のようになります。
const g = x => x.length;
const f = x => x === 4;
const isFourLetterWord = compose(f, g);射の中に恒等射と呼ばれる射があること
ここで、idと呼ばれる、便利な関数を導入しましょう。この関数は単純で、何か入力を受けたら、それをそのまま出力します。実際に関数を定義すると、次のようになります。
const id = x => x;ひょっとしたら、「これのどこが便利なんだろう?」と疑問に感じたかもしれません。
後のChapterで、この関数を様々な場所で使うことになるのですが、とりあえず、今は、値の代わりに使える関数(データのフリをした関数)だと考えてみましょう。
idとcomposeを組み合わせて使うときに、idは、1つの引数を持つ任意のfunction f に対して、次のような特別な性質を満たします。
// 恒等射
compose(id, f) === compose(f, id) === f;
// trueこの性質を満たす射のことを恒等射といいます。ですから、idは、この圏の恒等射になります。
さて、idは、まるで、数字における単位元(足し算における「0」、掛け算における「1」)のように見えます。もし、すぐに納得できないようであれば、少し時間をかけてみてください。
idは、そのうち様々な場面で使われることになります。ただ、現時点では、この関数は、与えられた値の代わりに振る舞うと考えておきましょう。この関数は、pointfree styleのコードを各ときには、とても役に立つことになります。
様々な圏
ここまでで、データ型と関数からなる圏を定義することができました。
とはいえ、もし、あなたが、圏論に始めて触れているのであれば、たぶん、圏とはどういうもので、なぜ役に立つのか、まだあまりピンと来ていないのではないかと思います。でも、これから、この本を通して知識を積み上げていきます。
とりあえず、このChapterでは、少なくとも、結合(composition)について、結合法則が成り立ち、恒等射が存在しているということは、わかったのではないかと思います。
そのほかに、どのような圏があるか気になるかもしれないので、いくつか例を挙げておきます。
-
有向グラフについて、「点の集合」を「対象」、「2つの点を結ぶ矢印」を「射」、「2つの点を結ぶ矢印をつなぐ」ことを「合成」とすると、圏を定義することができます
-
「数字」を「対象」、「≧」を「射」と定義することもできます(実際、任意の全順序集合や半順序集合から、圏を作ることができます)
このように、さまざまな圏がありますが、この本の目的を考えて、この本では、先ほど定義した「データ型と関数からなる圏」だけを考えていきます。
とりあえず、概要は掴めたと思いますので、次に進みましょう。
まとめ
関数の結合(composition)を使うと、まるで複数のパイプをつなぐように、関数を組み合わせて使えるようになります。そして、データは、あなたが作ったアプリケーションの中を流れていきます。
このとき、入力から出力まで、純粋関数でつないでいく必要があります。もし、このつながりを壊してしまった場合には、作ったソフトウエアは役に立たないものになってしまうでしょう。
アプリケーションを作るときには、結合(composition)を使うことを、設計の原則としましょう。
こうすることで、あなたが作るアプリケーションが単純かつ合理的なものになります。圏論は、アプリケーションの構造や、副作用の取り扱い方、正確な処理の保証に大きな役割を果たすでしょう。
次のChapterでは、ここまでの知識を実際に使って、実際にアプリケーションを作ってみましょう。
練習問題
https://mostly-adequate.gitbooks.io/mostly-adequate-guide/content/ch05.html#exercisesに移動して、問題を解いてみてください。